Kalman-Based Object Tracking with Low Signal/Noise Ratio

import os
os.chdir('YOURPATH')    # Set working directory
os. getcwd()

'''
This function generates the data for a 1D motion considering a
Piecewise constant, white noise acceleration model, equation (14)

var_q is the variance of the process noise
R is the variance of measurement noise
z is the measured data
x are the true values of the system states


'''

import sys
import numpy as np
import matplotlib.pyplot as plt
 
R = float('50')
N = 100 # data size
T = 1.0 # [s] Sampling time interval
A = np.array([[1, T], 
              [0, 1]], dtype=float)  # Transition matrix

def simulate(var_q):
    var_q = float(var_q)
    x = np.zeros((2, N)) # states are [position; speed; acceleration]
    x[:, 0] = [0, 10] # state initialization, change to give your own initial values
    G = np.array([[T**2/2], 
                  [T]], dtype=float) # Vector gain for the process noise
    w = np.random.normal(0.0, np.sqrt(var_q), N) # process noise
    for ii in range(1, N): # simulate system dynamics
      x[:, ii] = A.dot(x[:, ii-1]) + G.dot(w[ii]).T

    v = np.random.normal(0.0, np.sqrt(R), N) # measurement noise
    z = x[0, :] + v  # position measurements assuming C = [1 0 ]

    f1 = plt.figure()
    plt.plot(z, label='linear')
    plt.xlabel('Time [s]')
    plt.ylabel('Measured position')

    f2 = plt.figure()
    plt.plot(x[0,:], label='linear')
    plt.xlabel('Time [s]')
    plt.ylabel('True position [m]')

    f3 = plt.figure()
    plt.plot(x[1,:], label='linear')
    plt.xlabel('Time [s]')
    plt.ylabel('True speed [m/s]')

    return var_q, x, G, w, z 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

#t_states is true states
def apply_kf(t_states,z,R,var_q):
    NEES = np.zeros(N)
    NIS = np.zeros(N)
    S = np.zeros(N)
    # initial variables
    x = np.zeros((N+1,2,1))
    x[0][0][0]=z[0]
    x[0][0][0]=(z[1]-z[0])/T
    
    k = np.zeros((N,2,1))
    u = np.zeros(N)
    v = 0 
    C = np.array(np.mat('1 0'))    
    B = np.zeros((2,1))
    _p = np.zeros((N+1,2,2))
    
    #covariance
    p = np.zeros((N+1,2,2))
    init_p=np.array([[R,R/T],
                 [R/T,2*R/(T**2)]])
    # calculate the inverse of initial covariance matrix.
    p[0]=np.linalg.inv(init_p)
    
    for i in range(0,N):
        #Eq 5
        x[i+1] = A.dot(x[i]) + B.dot(u[i])
        #Eq 6
        _p[i] = A.dot(p[i]).dot(A.T) + G.dot(var_q).dot(G.T)
        #(Eq 7) Compute the Kalman gain
        k[i] = (_p[i].dot(C.T))/(np.dot(C.dot(_p[i]),C.T) + R)
        
        #Update the estimate and the error covariance
        #Eq 8
        x[i+1] = x[i+1]+k[i]*(z[i]-np.dot(C,x[i+1]))
        #Eq 9
        p[i+1] = np.dot(1-np.dot(k[i],C),_p[i])
        
        x_diff = np.reshape(t_states[:, i], (2,1))-x[i+1]       
        NEES[i] = np.dot(np.dot(x_diff.T,np.linalg.inv(p[i+1])),x_diff)
        S[i] = np.dot(np.dot(C,_p[i]),C.T)+R
        temp = z[i]-np.dot(C,x[i+1])
        NIS[i] = temp**2/S[i]
    return NEES,NIS,k,p,_p,x

(NEES,NIS,k,p,_p,_x) = apply_kf(x, z, R, float('1'))
plt.plot(_x[:,0],'r',linestyle='-',label='Estimated position')
plt.plot(x[0,:],'b', label='True position')
plt.xlabel('Time [s]') 
plt.ylabel('Position [m]')
plt.title('Q = 1')
plt.legend() 
plt.show()

plt.plot(_x[:,1],'r',label='Estimated speed')
plt.plot(x[1,:],'b', label='True speed')
plt.xlabel('Time [s]') 
plt.ylabel('Velocity[m/s]')
plt.title('Q = 1')
plt.legend() 
plt.show()

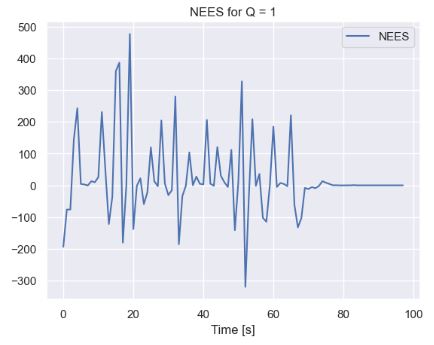
plt.plot(NEES[2::],label='NEES')
plt.title('NEES for Q = 1')
plt.xlabel('Time [s]')
plt.legend() 
plt.show()

plt.plot(NIS[0::],label='NIS')
plt.title('NIS for Q = 1')
plt.xlabel('Time [s]')
plt.legend() 
plt.show()

import numpy as np
from numpy.linalg import inv
import matplotlib.pyplot as plt

firstRun = True
x, P = np.array([[0,0]]).transpose(), np.zeros((2,2)) # X : Previous State Variable Estimation, P : Error Covariance Estimation
A, H = np.array([[0,0], [0,0]]), np.array([[0,0]])
Q, R = np.array([[0,0], [0,0]]), 0

def IntKalman(z):
    global firstRun
    global A, Q, H, R
    global x, P
    if firstRun:
        dt = 0.1
        A, Q = np.array([[1, dt], [0, 1]]), np.array([[1, 0], [0, 3]])
        # H, R = np.array([[1, 0]]),  np.array([10])
        H, R = np.array([[0, 1]]),  np.array([10])

        x = np.array([0, 80]).T
        P = 5 * np.eye(2)
        firstRun = False
    else:
        x_pred = A@x                              # x_pred : State Variable Prediction
        P_pred = A@P@A.T + Q                      # Error Covariance Prediction
        K = (P_pred@H.T) @ inv(H@P_pred@H.T + R)  # K : Kalman Gain
        x = x_pred + K@(z - H@x_pred)             # Update State Variable Estimation
        P = P_pred - K@H@P_pred                   # Update Error Covariance Estimation
    return x

# ------ Test program

np.random.seed(666)
Posp, Velp = None, None
def getVel(): #getPosSensor():
    global Posp, Velp
    if Posp == None:
        Posp = 0
        Velp = 80
    dt = 0.1

    # w = 0 + 10 * np.random.normal()
    v = 0 + 10 * np.random.normal()

    # z = Posp + Velp * dt + v  # Position measurement
    # Posp = z - v
    # Velp = 80 + w

    Posp = Posp + (Velp * dt)  # Position measurement
    z = Velp
    Velp = 80 + v
    print(f"v=>{v}")
    return z, Posp, Velp


time = np.arange(0, 10, 0.1)
Nsamples = len(time)

X_esti  = np.zeros([Nsamples, 2])
Z_saved = np.zeros([Nsamples, 2])

for i in range(Nsamples):
    Z, pos_true, vel_true = getVel()
    pos, vel = IntKalman(Z)

    X_esti[i]  = [pos, vel]
    Z_saved[i] = [pos_true, vel_true]
    
plt.figure()
plt.plot(time, Z_saved[:,1], 'b.', label = 'Measurements')
plt.plot(time, X_esti[:,1],  'r-', label='Kalman Filter')
plt.legend(loc='upper left')
plt.ylabel('Velocity [m/s]')
plt.xlabel('Time [sec]')

plt.figure()
plt.plot(time, Z_saved[:,0], 'b--', label='True Speed')
plt.plot(time, X_esti[:,0], 'r-', label='Kalman Filter')
plt.legend(loc='upper left')
plt.ylabel('Position [m]')
plt.xlabel('Time [sec]')
plt.show()

import numpy as np
import matplotlib.pyplot as plt
n=100
sz = (n) # size of array
t = np.linspace(0,10,n)
x = t + 2*t**2 # truth function
z = x + np.random.normal(0,7.5,size=sz) # noise

Q = 1e-3 # process variance

# allocate space for arrays
xhat=np.zeros(sz)      # a posteri estimate of x
P=np.zeros(sz)         # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz)    # a priori error estimate
K=np.zeros(sz)         # Kalman gain

R = 0.03**2 # estimate of measurement variance


xhat[0] = 0.0
P[0] = 1.0

for i in range(1,n):

  xhatminus[i] = xhat[i-1]
  Pminus[i] = P[i-1]+Q


  K[i] = Pminus[i]/( Pminus[i]+R )
  xhat[i] = xhatminus[i]+K[i]*(z[i]-xhatminus[i])
  P[i] = (1-K[i])*Pminus[i]

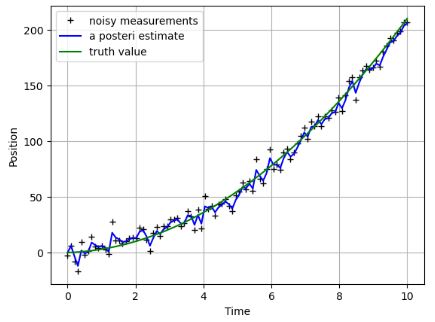
plt.figure()
plt.plot(t, z,'k+',label='noisy measurements')
plt.plot(t, xhat,'b-',label='a posteri estimate')
plt.plot(t,x,color='g',label='truth value')
plt.legend()
plt.xlabel('Time')
plt.ylabel('Position')
plt.grid()

plt.show()

import numpy as np 
import matplotlib.pyplot as plt
np.random.seed(123)
# KalmanFilter class definition
class KalmanFilter:
    def __init__(self, dt, initial_state, initial_covariance, transition_covariance, observation_covariance):
        self.dt = dt
        self.state = initial_state
        self.covariance = initial_covariance
        self.transition_covariance = transition_covariance
        self.observation_covariance = observation_covariance

        self.observation_matrix = np.array([[1, 0, 0, 0],
                                            [0, 1, 0, 0]])

    def predict(self, control_input=None):
        # Prediction step

        # State transition matrix
        A = np.array([[1, 0, self.dt, 0],
                      [0, 1, 0, self.dt],
                      [0, 0, 1, 0],
                      [0, 0, 0, 1]])

        # Control input matrix
        B = np.array([[0, 0, 0],
                      [0, 0.5 * self.dt ** 2, 0],
                      [0, 0, 0],
                      [0, self.dt, 0]])

        # Control input (acceleration)
        a = np.array([[0], [-9.8], [0]])

        # State prediction
        self.state = np.dot(A, self.state) + np.dot(B, a)

        # Covariance prediction
        self.covariance = np.dot(np.dot(A, self.covariance), A.T) + self.transition_covariance

    def update(self, measurement):
        # Update step

        # Observation matrix
        H = self.observation_matrix

        # Measurement residual
        y = measurement - np.dot(H, self.state)

        # Innovation covariance
        S = np.dot(np.dot(H, self.covariance), H.T) + self.observation_covariance
        # Kalman gain
        K = np.dot(np.dot(self.covariance, H.T), np.linalg.inv(S))

        # State update
        self.state = self.state + np.dot(K, y)

        I = np.eye(self.state.shape[0])  # Identity matrix

        # Covariance update
        self.covariance = np.dot((I - np.dot(K, H)), self.covariance)

    def get_state(self):
        return self.state

def simulate_ball_trajectory(launch_position, launch_speed, launch_angle, total_time=10.0, dt=0.1,
                             observation_time_step=0.5, observation_error_std=0.5, R_val=1, Q_val=1, 
                             skip_ob_start_time = 1.0, skip_ob_stop_time = 3.0, skip_observations = False):
    # Convert launch angle from degrees to radians
    launch_angle_rad = np.radians(launch_angle)

    # Calculate initial state based on launch position, launch speed, and launch angle
    initial_state = np.array([[launch_position[0]], [launch_position[1]],
                              [launch_speed * np.cos(launch_angle_rad)], [launch_speed * np.sin(launch_angle_rad)]])

    # Initialize the Kalman filter
    filter = KalmanFilter(dt, initial_state, np.eye(4), np.array([[R_val, 0, 0, 0], [0, R_val, 0, 0],
                                                                  [0, 0, R_val, 0], [0, 0, 0, R_val]]),
                          np.array([[Q_val, 0], [0, Q_val]]))

    time = np.arange(0, total_time, dt)
    observations = []
    actual_velocities = []
    predicted_velocities = []
    predicted_observations = []
    true_positions = []  # List to store true positions

    for t in time:
            
        # Simulate ball trajectory (example: simple parabolic motion in x and y directions)
        position_x = initial_state[0, 0] + initial_state[2, 0] * dt
        position_y = initial_state[1, 0] + initial_state[3, 0] * dt + 0.5 * (-9.8) * dt ** 2
        velocity_x = initial_state[2, 0]
        velocity_y = initial_state[3, 0] + (-9.8) * dt
        
        # Simulate observation (with noise)
        if skip_observations and skip_ob_start_time <= t <= skip_ob_stop_time:
            observation = np.array([[observations[-1][0]], [observations[-1][1]]])
        else:
            observation = np.array([[position_x + np.random.normal(0, observation_error_std)],
                                    [position_y + np.random.normal(0, observation_error_std)]])

        
        # Update filter with observation
        filter.predict()
        filter.update(observation)

        # Store estimated state
        estimated_state = filter.get_state()
        
        # Store true position
        true_positions.append([position_x, position_y])

        # Print actual observation, predicted observation, actual velocity (X and Y), and predicted velocity (X and Y)
        print(f"Time: {t:.2f}")
        print(f"Actual Observation: {observation.flatten()}")
        print(f"Predicted Observation: {np.dot(filter.observation_matrix, estimated_state).flatten()}")
        print(f"Actual Velocity (X, Y): ({velocity_x:.2f}, {velocity_y:.2f})")
        print(f"Predicted Velocity (X, Y): ({estimated_state[2, 0]:.2f}, {estimated_state[3, 0]:.2f})")
        print()

        # Adjust initial state for the next iteration
        initial_state = estimated_state
        observations.append(observation.flatten())
        actual_velocities.append([velocity_x, velocity_y])
        predicted_velocities.append([estimated_state[2, 0], estimated_state[3, 0]])
        predicted_observations.append(np.dot(filter.observation_matrix, estimated_state).flatten()[1])

        # Adjust initial state for the next iteration
        initial_state = estimated_state

    # Convert observations, actual velocities, predicted velocities, predicted observations, and true positions to numpy arrays
    observations = np.array(observations)
    actual_velocities = np.array(actual_velocities)
    predicted_velocities = np.array(predicted_velocities)
    predicted_observations = np.array(predicted_observations)
    true_positions = np.array(true_positions)


    
     # Plot observations, velocities, and true trajectory
    plt.figure(figsize=(10, 6))

    plt.plot(time, observations[:, 1], 'bo', label='Actual Y Observation', markersize=5)
    plt.plot(time, predicted_observations, 'k--', label='Predicted Y Observation')
    plt.plot(time, actual_velocities[:, 0], 'C2--', label='Actual X Velocity')
    plt.plot(time, actual_velocities[:, 1], 'C1--', label='Actual Y Velocity')
    plt.plot(time, predicted_velocities[:, 0], 'C2', label='Predicted X Velocity')
    plt.plot(time, predicted_velocities[:, 1], 'C1', label='Predicted Y Velocity')
    plt.plot(time, true_positions[:, 1], 'r', label='True Y Position', linewidth=2)

    plt.xlabel('Time', fontsize=12)
    plt.ylabel('Observation / Velocity / Position', fontsize=12)
    plt.title('Ball Trajectory Simulation', fontsize=14)
    plt.legend(fontsize=10)

    plt.grid(True)
    plt.tight_layout()
    plt.show()
    
    
    return observations, predicted_observations
    

def calculate_accuracy(actual_values, predicted_values):
    rmse = np.sqrt(np.mean((actual_values[:, 1] - predicted_values) ** 2))
    mae = np.mean(np.abs(actual_values[:, 1] - predicted_values))
    return rmse, mae

class CondensationFilter:
    def __init__(self, dt, num_particles, initial_state, initial_covariance, transition_covariance, observation_covariance):
        self.dt = dt
        self.num_particles = num_particles
#         self.particles = [initial_state + np.random.multivariate_normal(np.zeros(initial_state.shape), initial_covariance).reshape(-1, 1) for _ in range(num_particles)]
        self.particles = [initial_state + np.random.multivariate_normal(np.zeros(initial_state.shape[0]), initial_covariance).reshape((-1, 1)) for _ in range(num_particles)]

        self.weights = np.ones(num_particles) / num_particles
        self.transition_covariance = transition_covariance
        self.observation_covariance = observation_covariance

        self.observation_matrix = np.array([[1, 0, 0, 0],
                                            [0, 1, 0, 0]])

    def predict(self, control_input=None):
        # Prediction step

        # State transition matrix
        A = np.array([[1, 0, self.dt, 0],
                      [0, 1, 0, self.dt],
                      [0, 0, 1, 0],
                      [0, 0, 0, 1]])

        # Control input matrix
        B = np.array([[0, 0, 0],
                      [0, 0.5 * self.dt ** 2, 0],
                      [0, 0, 0],
                      [0, self.dt, 0]])

        # Control input (acceleration)
        a = np.array([[0], [-9.8], [0]])

        # State prediction
        self.particles = [np.dot(A, particle) + np.dot(B, a) + np.random.multivariate_normal(np.zeros(particle.shape[0]), self.transition_covariance) for particle in self.particles]

    def update(self, measurement):
        # Update step

        # Observation matrix
        H = self.observation_matrix

        for i, particle in enumerate(self.particles):
            # Measurement residual
            y = measurement - np.dot(H, particle)

            # Particle weight update
            self.weights[i] = np.exp(-0.5 * np.dot(np.dot(y.T, np.linalg.inv(self.observation_covariance)), y))[0, 0]

        
        # Normalize weights and handle NaN values
        self.weights /= np.sum(self.weights)
        self.weights[np.isnan(self.weights)] = np.finfo(float).eps
        self.weights /= np.sum(self.weights)

        # Resampling
        indices = np.random.choice(np.arange(self.num_particles), size=self.num_particles, p=self.weights)
        self.particles = [self.particles[index] for index in indices]
        self.weights = np.ones(self.num_particles) / self.num_particles


    def get_state(self):
        return np.mean(np.concatenate(self.particles, axis=1), axis=1).reshape((-1, 1))

def simulate_ball_trajectory_particle(launch_position, launch_speed, launch_angle, no_particles=100, total_time=10.0, dt=0.1,
                             observation_time_step=0.5, observation_error_std=0.5, R_val=1, Q_val=1,
                             skip_ob_start_time=1.0, skip_ob_stop_time=3.0, skip_observations=False):
    # Convert launch angle from degrees to radians
    launch_angle_rad = np.radians(launch_angle)

    # Calculate initial state based on launch position, launch speed, and launch angle
    initial_state = np.array([[launch_position[0]], [launch_position[1]],
                              [launch_speed * np.cos(launch_angle_rad)], [launch_speed * np.sin(launch_angle_rad)]])

    # Initialize the Condensation Filter
    filter = CondensationFilter(dt, num_particles=no_particles, initial_state=initial_state, initial_covariance=np.eye(4),
                                transition_covariance=np.array([[R_val, 0, 0, 0], [0, R_val, 0, 0],
                                                               [0, 0, R_val, 0], [0, 0, 0, R_val]]),
                                observation_covariance=np.array([[Q_val, 0], [0, Q_val]]))

    time = np.arange(0, total_time, dt)
    observations = []
    actual_velocities = []
    predicted_velocities = []
    predicted_observations = []
    true_positions = []  # List to store true positions

    # Initialize a list to store particle trajectories
    particle_trajectories = [[] for _ in range(filter.num_particles)]
    particle_weights = [[] for _ in range(filter.num_particles)]

    for t in time:
#         # Check if skipping new observations is required
#         if t >= skip_ob_start_time and t <= skip_ob_stop_time:
#             skip_observations = True
#         else:
#             skip_observations = False

        # Simulate ball trajectory (example: simple parabolic motion in x and y directions)
        position_x = initial_state[0, 0] + initial_state[2, 0] * dt
        position_y = initial_state[1, 0] + initial_state[3, 0] * dt + 0.5 * (-9.8) * dt ** 2
        velocity_x = initial_state[2, 0]
        velocity_y = initial_state[3, 0] + (-9.8) * dt

        # Simulate observation (with noise)
        if skip_observations and skip_ob_start_time <= t <= skip_ob_stop_time:
            observation = np.array([[observations[-1][0]], [observations[-1][1]]])
        else:
            observation = np.array([[position_x + np.random.normal(0, observation_error_std)],
                                    [position_y + np.random.normal(0, observation_error_std)]])

        # Update filter with observation
        filter.predict()
        filter.update(observation)

        # Store estimated state
        estimated_state = filter.get_state()

        # Store true position
        true_positions.append([position_x, position_y])

        # Print actual observation, predicted observation, actual velocity (X and Y), and predicted velocity (X and Y)
        print(f"Time: {t:.2f}")
        print(f"Actual Observation: {observation.flatten()}")
        print(f"Predicted Observation: {np.dot(filter.observation_matrix, estimated_state).flatten()}")
        print(f"Actual Velocity (X, Y): ({velocity_x:.2f}, {velocity_y:.2f})")
        print(f"Predicted Velocity (X, Y): ({estimated_state[2, 0]:.2f}, {estimated_state[3, 0]:.2f})")
        print()

        # Adjust initial state for the next iteration
        initial_state = estimated_state
        observations.append(observation.flatten())
        actual_velocities.append([velocity_x, velocity_y])
        predicted_velocities.append([estimated_state[2, 0], estimated_state[3, 0]])
        predicted_observations.append(np.dot(filter.observation_matrix, estimated_state).flatten())

        # Adjust initial state for the next iteration
        initial_state = estimated_state

        # Store particle positions and weights for trajectory plot
        for i in range(filter.num_particles):
            particle_trajectories[i].append(filter.particles[i][1])
            particle_weights[i].append(filter.weights[i])

    # Convert lists to numpy arrays
    particle_trajectories = np.array(particle_trajectories)
    particle_weights = np.array(particle_weights)

    # Convert observations, actual velocities, predicted velocities, predicted observations, and true positions to numpy arrays
    observations = np.array(observations)
    actual_velocities = np.array(actual_velocities)
    predicted_velocities = np.array(predicted_velocities)
    predicted_observations = np.array(predicted_observations)
    true_positions = np.array(true_positions)

    # Plot observations, velocities, and true trajectory
    plt.figure(figsize=(12, 8))
    plt.plot(time, observations[:, 1], 'bo', label='Actual Y Observation')
    plt.plot(time, predicted_observations[:, 1], 'k--', label='Predicted Y Observation')
    # plt.plot(time, actual_velocities[:, 0], 'b--', label='Actual X Velocity')
    # plt.plot(time, actual_velocities[:, 1], 'r--', label='Actual Y Velocity')
    # plt.plot(time, predicted_velocities[:, 0], 'y', label='Predicted X Velocity')
    # plt.plot(time, predicted_velocities[:, 1], 'g', label='Predicted Y Velocity')
    plt.plot(time, true_positions[:, 1], 'r', label='True Y Position')  # Plotting true Y positions
    plt.xlabel('Time')
    plt.ylabel('Observation / Position')
    plt.legend()

    # Plot particles and their weights
    plt.figure(figsize=(8, 6))
    for i in range(filter.num_particles):
        particle_trajectory = particle_trajectories[i]
        weights = particle_weights[i]
        alpha = weights.tolist()[0] * 15  # Convert weights array to list and take the first element
    plt.plot(time, particle_trajectory, "ro" , alpha=alpha)
    plt.xlabel('Time')
    plt.ylabel('Y Position')
    plt.title('Particles and their Weights')
    plt.tight_layout()
    plt.show()
    return observations, predicted_observations

def calculate_accuracy_particle(actual_values, predicted_values):
    rmse = np.sqrt(np.mean((actual_values[:, 1] - predicted_values[:, 1]) ** 2))
    mae = np.mean(np.abs(actual_values[:, 1] - predicted_values[:, 1]))
    return rmse, mae

def simulate_ball_trajectory_particle_2balls(launch_position, launch_speed, launch_angle, launch_position2, launch_speed2, launch_angle2,
                             no_particles=100, total_time=10.0, dt=0.1, observation_time_step=0.5,
                             observation_error_std=0.5, R_val=1, Q_val=1, skip_ob_start_time=1.0,
                             skip_ob_stop_time=3.0, skip_observations=False):
    
    # Convert launch angles from degrees to radians
    launch_angle_rad = np.radians(launch_angle)
    launch_angle_rad2 = np.radians(launch_angle2)

    # Calculate initial states based on launch positions, launch speeds, and launch angles
    initial_state = np.array([[launch_position[0]], [launch_position[1]],
                              [launch_speed * np.cos(launch_angle_rad)], [launch_speed * np.sin(launch_angle_rad)]])
    initial_state2 = np.array([[launch_position2[0]], [launch_position2[1]],
                               [launch_speed2 * np.cos(launch_angle_rad2)], [launch_speed2 * np.sin(launch_angle_rad2)]])

    # Initialize the Condensation Filters
    filter = CondensationFilter(dt, num_particles=no_particles, initial_state=initial_state, initial_covariance=np.eye(4),
                                transition_covariance=np.array([[R_val, 0, 0, 0], [0, R_val, 0, 0],
                                                               [0, 0, R_val, 0], [0, 0, 0, R_val]]),
                                observation_covariance=np.array([[Q_val, 0], [0, Q_val]]))

    filter2 = CondensationFilter(dt, num_particles=no_particles, initial_state=initial_state2,
                                 initial_covariance=np.eye(4),
                                 transition_covariance=np.array([[R_val, 0, 0, 0], [0, R_val, 0, 0],
                                                                [0, 0, R_val, 0], [0, 0, 0, R_val]]),
                                 observation_covariance=np.array([[Q_val, 0], [0, Q_val]]))

    time = np.arange(0, total_time, dt)

    # Initialize lists to store observations, velocities, predicted observations, and true positions for both balls
    observations1 = []
    actual_velocities1 = []
    predicted_velocities1 = []
    predicted_observations1 = []
    true_positions1 = []

    observations2 = []
    actual_velocities2 = []
    predicted_velocities2 = []
    predicted_observations2 = []
    true_positions2 = []

    # Initialize lists to store particle trajectories and weights for both balls
    particle_trajectories1 = [[] for _ in range(filter.num_particles)]
    particle_weights1 = [[] for _ in range(filter.num_particles)]

    particle_trajectories2 = [[] for _ in range(filter2.num_particles)]
    particle_weights2 = [[] for _ in range(filter2.num_particles)]

    for t in time:
        # Check if skipping new observations is required
#         if t >= skip_ob_start_time and t <= skip_ob_stop_time:
#             skip_observations = True
#         else:
#             skip_observations = False

        # Simulate ball 1 trajectory (example: simple parabolic motion in x and y directions)
        position_x1 = initial_state[0, 0] + initial_state[2, 0] * dt
        position_y1 = initial_state[1, 0] + initial_state[3, 0] * dt + 0.5 * (-9.8) * dt ** 2
        velocity_x1 = initial_state[2, 0]
        velocity_y1 = initial_state[3, 0] + (-9.8) * dt

        # Simulate ball 2 trajectory (example: simple parabolic motion in x and y directions)
        position_x2 = initial_state2[0, 0] + initial_state2[2, 0] * dt
        position_y2 = initial_state2[1, 0] + initial_state2[3, 0] * dt + 0.5 * (-9.8) * dt ** 2
        velocity_x2 = initial_state2[2, 0]
        velocity_y2 = initial_state2[3, 0] + (-9.8) * dt

        # Simulate observations for ball 1 (with noise)
        if skip_observations and skip_ob_start_time <= t <= skip_ob_stop_time:
            observation1 = np.array([[observations1[-1][0]], [observations1[-1][1]]])
        else:
            observation1 = np.array([[position_x1 + np.random.normal(0, observation_error_std)],
                                    [position_y1 + np.random.normal(0, observation_error_std)]])

        # Simulate observations for ball 2 (with noise)
        if skip_observations and skip_ob_start_time <= t <= skip_ob_stop_time:
            observation2 = np.array([[observations2[-1][0]], [observations2[-1][1]]])
        else:
            observation2 = np.array([[position_x2 + np.random.normal(0, observation_error_std)],
                                    [position_y2 + np.random.normal(0, observation_error_std)]])

        # Update filter 1 with observation 1
        filter.predict()
        filter.update(observation1)

        # Update filter 2 with observation 2
        filter2.predict()
        filter2.update(observation2)

        # Store estimated states for both balls
        estimated_state1 = filter.get_state()
        estimated_state2 = filter2.get_state()

        # Store true positions for both balls
        true_positions1.append([position_x1, position_y1])
        true_positions2.append([position_x2, position_y2])

        # Print actual observation, predicted observation, actual velocity (X and Y),
        # and predicted velocity (X and Y) for both balls
        print(f"Time: {t:.2f}")
        print("Ball 1:")
        print(f"Actual Observation: {observation1.flatten()}")
        print(f"Predicted Observation: {np.dot(filter.observation_matrix, estimated_state1).flatten()}")
        print(f"Actual Velocity (X, Y): ({velocity_x1:.2f}, {velocity_y1:.2f})")
        print(f"Predicted Velocity (X, Y): ({estimated_state1[2, 0]:.2f}, {estimated_state1[3, 0]:.2f})")
        print()
        print("Ball 2:")
        print(f"Actual Observation: {observation2.flatten()}")
        print(f"Predicted Observation: {np.dot(filter2.observation_matrix, estimated_state2).flatten()}")
        print(f"Actual Velocity (X, Y): ({velocity_x2:.2f}, {velocity_y2:.2f})")
        print(f"Predicted Velocity (X, Y): ({estimated_state2[2, 0]:.2f}, {estimated_state2[3, 0]:.2f})")
        print()

        # Adjust initial states for the next iteration
        initial_state = estimated_state1
        initial_state2 = estimated_state2

        # Store observations, velocities, predicted observations, and estimated states for both balls
        observations1.append(observation1.flatten())
        observations2.append(observation2.flatten())

        actual_velocities1.append([velocity_x1, velocity_y1])
        actual_velocities2.append([velocity_x2, velocity_y2])

        predicted_velocities1.append([estimated_state1[2, 0], estimated_state1[3, 0]])
        predicted_velocities2.append([estimated_state2[2, 0], estimated_state2[3, 0]])

        predicted_observations1.append(np.dot(filter.observation_matrix, estimated_state1).flatten())
        predicted_observations2.append(np.dot(filter2.observation_matrix, estimated_state2).flatten())

        # Store particle positions and weights for trajectory plot for both balls
        for i in range(filter.num_particles):
            particle_trajectories1[i].append(filter.particles[i][1])
            particle_weights1[i].append(filter.weights[i])

        for i in range(filter2.num_particles):
            particle_trajectories2[i].append(filter2.particles[i][1])
            particle_weights2[i].append(filter2.weights[i])

    # Convert lists to numpy arrays for both balls
    particle_trajectories1 = np.array(particle_trajectories1)
    particle_weights1 = np.array(particle_weights1)

    particle_trajectories2 = np.array(particle_trajectories2)
    particle_weights2 = np.array(particle_weights2)

    observations1 = np.array(observations1)
    actual_velocities1 = np.array(actual_velocities1)
    predicted_velocities1 = np.array(predicted_velocities1)
    predicted_observations1 = np.array(predicted_observations1)
    true_positions1 = np.array(true_positions1)

    observations2 = np.array(observations2)
    actual_velocities2 = np.array(actual_velocities2)
    predicted_velocities2 = np.array(predicted_velocities2)
    predicted_observations2 = np.array(predicted_observations2)
    true_positions2 = np.array(true_positions2)

    # Plot observations, velocities, and true trajectory for both balls
    plt.figure(figsize=(12, 8))
    plt.plot(time, observations1[:, 1], 'bo', label='Ball 1: Actual Y Observation')
    plt.plot(time, predicted_observations1[:, 1], '--g', label='Ball 1: Predicted Y Observation')
    plt.plot(time, true_positions1[:, 1], 'y', label='Ball 1: True Y Position')
    plt.plot(time, observations2[:, 1], 'ro', label='Ball 2: Actual Y Observation')
    plt.plot(time, predicted_observations2[:, 1], '--g', label='Ball 2: Predicted Y Observation')
    plt.plot(time, true_positions2[:, 1], 'y', label='Ball 2: True Y Position')
    plt.xlabel('Time')
    plt.ylabel('Observation / Position')
    plt.legend()

    # Plot particle trajectories and their weights for both balls
    plt.figure(figsize=(8, 6))
    for i in range(filter.num_particles):
        particle_trajectory = particle_trajectories1[i]
        weights = particle_weights1[i]
        alpha = weights.tolist()[0] * 3
        plt.plot(time, particle_trajectory, "bo", alpha=alpha)
    for i in range(filter2.num_particles):
        particle_trajectory = particle_trajectories2[i]
        weights = particle_weights2[i]
        alpha = weights.tolist()[0] * 3
        plt.plot(time, particle_trajectory, "ro", alpha=alpha)
    plt.xlabel('Time')
    plt.ylabel('Particle Trajectory')
    plt.show()
    return observations1, predicted_observations1, observations2, predicted_observations2

def calculate_accuracy_particle_2_balls(actual_values1, predicted_values1, actual_values2, predicted_values2):
    rmse1 = np.sqrt(np.mean((actual_values1[:, 1] - predicted_values1[:, 1]) ** 2))
    mae1 = np.mean(np.abs(actual_values1[:, 1] - predicted_values1[:, 1]))
    rmse2 = np.sqrt(np.mean((actual_values2[:, 1] - predicted_values2[:, 1]) ** 2))
    mae2 = np.mean(np.abs(actual_values2[:, 1] - predicted_values2[:, 1]))
    return rmse1, mae1, rmse2, mae2

#Differenet Launch positions
mean_P = 0
sd_P = 1
mean_Q = 0
sd_Q = 1
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 4.5
launch_position = [10,10]
launch_speed = 100
launch_angle = 45
start_ob_time = 2
stop_ob_time = 7
skip_observations = False

observations, predicted_observations= simulate_ball_trajectory(launch_position, launch_speed, launch_angle, total_time=10.0, dt=0.1, 
                                                                                                                         observation_time_step=0.5, 
    observation_error_std=Observation_noise, skip_ob_start_time = start_ob_time,skip_ob_stop_time = stop_ob_time, skip_observations = skip_observations)  
 

# Measure the accuracy of the estimated observations and velocities
obs_rmse, obs_mae = calculate_accuracy(observations, predicted_observations)

# Print the accuracy metrics
print("Observation Loss:")
print(f"RMSE: {obs_rmse:.2f}")
print(f"MAE: {obs_mae:.2f}")

Observation Loss:
RMSE: 1.39
MAE: 1.10

mean_P = 0
sd_P = 1
mean_Q = 0
sd_Q = 1
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 4.5
launch_position = [30, 50]
launch_speed = 100
launch_angle = 45
start_ob_time = 2
stop_ob_time = 7
skip_observations = False
observations, predicted_observations= simulate_ball_trajectory(launch_position, launch_speed, launch_angle, total_time=10.0, dt=0.1, 
                                                                                                                         observation_time_step=0.5, 
    observation_error_std=Observation_noise, skip_ob_start_time = start_ob_time,skip_ob_stop_time = stop_ob_time, skip_observations = skip_observations)  
 

mean_P = 0
sd_P = 1
mean_Q = 0
sd_Q = 1
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 4.5
launch_position = [20, 50]
launch_speed = 100
launch_angle = 45
start_ob_time = 2
stop_ob_time = 7
skip_observations = False

observations, predicted_observations= simulate_ball_trajectory(launch_position, launch_speed, launch_angle, total_time=20.0, dt=0.5, 
                                                                                                                         observation_time_step=0.5,
                                                                   observation_error_std=Observation_noise, skip_ob_start_time = start_ob_time,skip_ob_stop_time = stop_ob_time, skip_observations = skip_observations)
    

mean_P = 0
sd_P = 1
mean_Q = 0
sd_Q = 1
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 8.5
launch_position = [10,10]
launch_speed = 100
launch_angle = 45
start_ob_time = 5
stop_ob_time = 7
skip_observations = True

observations, predicted_observations= simulate_ball_trajectory(launch_position, launch_speed, launch_angle, total_time=20.0, dt=0.5, 
                                                                                                                         observation_time_step=0.5,
                                                                   observation_error_std=Observation_noise, skip_ob_start_time = start_ob_time,skip_ob_stop_time = stop_ob_time, skip_observations = skip_observations)

mean_P = 0
sd_P = 1
mean_Q = 0
sd_Q = 1
no_particles = 500
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 5
launch_position = [-50,-30]
launch_speed = 100
launch_angle = 45
start_ob_time = 4
stop_ob_time = 6
skip_observations = True
observations_ball1_1, predicted_observations_ball1_1 = simulate_ball_trajectory_particle(launch_position, launch_speed, launch_angle, no_particles=100, total_time=10.0, dt=0.1,
                             observation_time_step=0.5, observation_error_std=0.5, R_val=1, Q_val=1,
                             skip_ob_start_time=start_ob_time, skip_ob_stop_time=stop_ob_time, skip_observations=True)

# Measure the accuracy of the estimated observations and velocities
obs_rmse, obs_mae = calculate_accuracy_particle(observations_ball1_1, predicted_observations_ball1_1)

# Print the accuracy metrics
print("Observation Loss:")
print(f"RMSE: {obs_rmse:.2f}")
print(f"MAE: {obs_mae:.2f}")
print()

Observation Loss:
RMSE: 5.43
MAE: 2.81

mean_P = 0
sd_P = 10
mean_Q = 0
sd_Q = 10
no_particles = 500
P = np.random.normal(mean_P, sd_P)
Q = np.random.normal(mean_Q, sd_Q)
Observation_noise = 25
launch_position = [100,100]
launch_speed = 30
launch_angle = 45
launch_position2 = [-300, -300]
launch_speed2 = 100
launch_angle2 = 45
start_ob_time = 4
stop_ob_time = 6
skip_observations = True
observations_ball2_1, predicted_observations_ball2_1, observations_ball2_2, predicted_observations_ball2_2 = simulate_ball_trajectory_particle_2balls(launch_position, launch_speed, launch_angle, launch_position2, launch_speed2, launch_angle2,
                             no_particles=100, total_time=10.0, dt=0.1, observation_time_step=0.5,
                             observation_error_std=0.5, R_val=1, Q_val=1, skip_ob_start_time=start_ob_time,
                             skip_ob_stop_time=stop_ob_time, skip_observations=False)
        

# Measure the accuracy of the estimated observations and velocities
rmse1, mae1, rmse2, mae2 = calculate_accuracy_particle_2_balls(observations_ball2_1, predicted_observations_ball2_1, observations_ball2_2, predicted_observations_ball2_2)

# Print the accuracy metrics
print("Observation Loss ball 1:")
print(f"RMSE: {rmse1:.2f}")
print(f"MAE: {mae1:.2f}")
print("Observation Loss ball 2:")
print(f"RMSE: {rmse2:.2f}")
print(f"MAE: {mae2:.2f}")
print()

Observation Loss ball 1:
RMSE: 0.75
MAE: 0.57
Observation Loss ball 2:
RMSE: 1.67
MAE: 0.92

from pylab import *
import numpy as np

def ROVsimulation(procVar,measVar,N,dt):
	#DO NOT CHANGE
	# Function Given for creating simulated data
	acc = zeros((2,N))
	vel = zeros((2,N))
	control_acc = zeros((2,N))
	pos = zeros((2,N))
	meas_pos = zeros((2,N))
	z = zeros((2,N))
	for i in arange(1,N):
		z = normal([0, 0], 0.1)- 0.05*control_acc[:,i-1]
		control_acc[:,i] = control_acc[:,i-1] + z - 0.01*vel[:,i-1]
		vel[:,i] = vel[:,i-1] + control_acc[:,i-1]*dt
		pos[:,i] = pos[:,i-1] + vel[:,i-1]*dt + control_acc[:,i-1]*0.5*dt**2

	acc = normal(control_acc, sqrt(procVar))
	pos = zeros((2,N))
	vel = zeros((2,N))

	for i in arange(1,N):

		vel[:,i] = vel[:,i-1] + acc[:,i-1]*dt
		pos[:,i] = pos[:,i-1] + vel[:,i-1]*dt + acc[:,i-1]*0.5*dt**2


	meas_pos = normal(pos, sqrt(measVar))
	real_pos = pos

	return control_acc, meas_pos, real_pos


def predict(control_acc, dt, procVar , X, P, i):
        F = [[1,dt,0,0], [0,0,0,0], [0,0,1,dt], [0,0,0,0]]
        B = [[0,0],[1,0],[0,0],[0,1]]
        Q = [[procVar,0,0,0],[0,0,0,0],[0,0,procVar,0],[0,0,0,0]]
        X = np.add(np.matmul(F, X), np.matmul(B, control_acc[:,i-1]))
        P = np.add(np.matmul(np.matmul(F, P), np.transpose(F)),Q)
        return X, P

def update( meas_pos, dt, measVar, X, P, i):
        H = [[1,0,0,0],[0,0,1,0]]
        R = [[measVar,0],[0,measVar]]
        K1 = np.matmul(np.matmul(P, np.transpose(H)), np.linalg.inv(np.add(np.matmul(np.matmul(H, P), np.transpose(H)), R)))
        X = np.add(X, np.matmul(K1, np.subtract(meas_pos[:,i], np.matmul(H, X))))
        P = np.subtract(P, np.matmul(np.matmul(K1, H), P))
        return X, P



def your_KalmanFilter(control_acc,meas_pos,procVar,measVar,N,dt):
############################################################################################
#TODO: design kalman filter
#MODEL: position = position + velocity*time_interval + 0.5*acceleration*time_interval**2
#############################################################################################
        approx_pos = zeros((2,N))
        X = [meas_pos[0][0], 1, meas_pos[1][0], 0]
        P = [[0,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,0]]
        for i in range(1, len(control_acc[0])):
                X, P = predict(control_acc, dt, procVar, X, P, i)
                X, P = update(meas_pos, dt, measVar, X, P, i)
                approx_pos[0][i] = X[0]
                approx_pos[1][i] = X[2]
        return approx_pos

##############################
#Code starts here
##############################
N = int(1e4)				# number of simulation sample point
dt = 1.0/100.0		# time interval for each sample point
procVar = 0.001		# Process(Prediction) Noise
measVar = 3			# Measurement Noise

[control_acc, meas_pos, real_pos] = ROVsimulation(procVar,measVar,N,dt)
#control_acc: acceleration as a control input signal to the filter
#meas_pos: position measurement
#real_pos: actual position of vehicle(not observable)

approx_pos = your_KalmanFilter(control_acc, meas_pos, procVar, measVar, N, dt)


figure()
plot(approx_pos[0,:],approx_pos[1,:], 'r',label = 'Approx Position')
#plot(meas_pos[0,:],meas_pos[1,:], 'g',label = 'Measured Position')
plot(real_pos[0,:],real_pos[1,:],'b',label = 'True Position')
show()

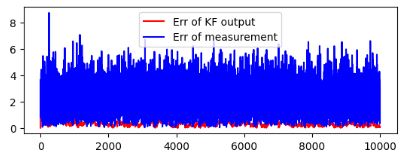
# Plotting error from real value
figure()
subplot(2,1,1)
plot(norm(approx_pos[:,:]-real_pos[:,:],axis=0), 'r',label = 'Err of KF output')
plot(norm(meas_pos[:,:]-real_pos[:,:],axis=0),'b',label = 'Err of measurement')
legend()
show()
Kalman-based simulation of 2D trajectories: red label is the Approximate Position and blue label is the true trajectory:

import numpy as np
from math import sin, cos
import matplotlib.pyplot as plt


class KalmanFilter:
    def __init__(self, x, r=np.eye(4), q=np.eye(4)):
        self.x = x
        self.P = np.eye(3)
        self.H = np.eye(3)
        self.Q = q
        self.R = r

        self.state_hist = np.array([self.x.copy()])

    def F(self, v=0., w=0., ang=0.):
        F = np.eye(3)
        F[0, 2] = -(v * sin(ang))
        F[1, 2] = v * cos(ang)
        F[2, 2] = 0.
        return F

    def motion_model(self, prev, ctl):
        x = prev[0]
        y = prev[1]
        thet = prev[2]

        v = ctl[0]
        w = ctl[1]

        x_k1 = x + (v * cos(thet) * DT)
        y_k1 = y + (v * sin(thet) * DT)
        thet_k1 = thet + (w * DT)

        return np.array([x_k1, y_k1, thet_k1])

    def predict(self, controls=np.zeros(2)):
        F = self.F(controls[0], controls[1], self.x[2])
        self.x = self.motion_model(self.x, controls)
        self.P = F @ self.P @ F.T + self.Q

    def update(self, z):
        K2 = np.linalg.inv(self.H @ self.P @ self.H.T + self.R)
        K = self.P @ self.H.T @ K2

        self.x += K @ (z - self.H @ self.x)
        self.P = (np.eye(3) - K @ self.H) @ self.P

        self.state_hist = np.vstack((self.state_hist, self.x))

    def __call__(self, controls, z):
        self.predict(controls)
        self.update(z)


def update(states, controls):
    pos_noise = np.random.normal(0., .1, 2)
    thet_noise = np.random.normal(0., .1, 1)

    states[0] += ((controls[0] * cos(states[2])) * DT) + pos_noise[0]
    states[1] += ((controls[0] * sin(states[2])) * DT) + pos_noise[1]
    states[2] += (controls[1] * DT) + thet_noise[0]


# Must pass a copy of 'states' to this
def sense_state(states):
    pos_noise = np.random.normal(0., .075, 2)
    thet_noise = np.random.normal(0., .075, 1)

    states[0] += pos_noise[0]
    states[1] += pos_noise[1]
    states[2] += thet_noise[0]

    return states


if __name__ == "__main__":
    DT = .1
    #                      x   y  thet
    true_state = np.array([0., .5, 0.])
    true_state_hist = [true_state.copy()]

    cov_est = np.zeros((3, 3))
    cmd = np.array([1.5, 0.35])

    q_mat = np.eye(3) * .1  # Motion Model
    r_mat = np.eye(3) * .025  # Sensor Model
    init_measured_state = sense_state(true_state.copy())
    kf = KalmanFilter(init_measured_state, q_mat, r_mat)
    measured_state_hist = [init_measured_state.copy()]

    err = 0.
    measured_err = 0.

    for i in range(100):
        update(true_state, cmd)
        measured_state = sense_state(true_state.copy())
        kf(cmd, measured_state)
        true_state_hist.append(true_state.copy())
        measured_state_hist.append(measured_state.copy())
        err += np.sum(np.abs(true_state - kf.x))
        measured_err += np.sum(np.abs(true_state - measured_state))

    true_state_hist = np.array(true_state_hist)
    measured_state_hist = np.array(measured_state_hist)

    print("True State: ", [round(ts, 3) for ts in true_state])
    print("KF State: ", [round(xi, 3) for xi in kf.x])
    print("KF Covariance: ")
    print(kf.P)

    print("--------------------------------------")
    print("Kalman Filter Err: ", err)
    print("Measured Err: ", measured_err)

    plt.plot(true_state_hist[:, 0], true_state_hist[:, 1], 'r--', label="True")
    plt.plot(kf.state_hist[:, 0], kf.state_hist[:, 1], 'b--', label="Kalman Filter")
    plt.plot(measured_state_hist[:, 0], measured_state_hist[:, 1], 'gx', label="Measured")
    plt.grid()
    plt.legend()
    plt.xlim(-5., 15.)
    plt.ylim(0., 15.)
    plt.show()

True State:  [-2.606, 7.399, 3.532]
KF State:  [-2.549, 7.388, 3.573]
KF Covariance: 
[[ 0.04158589 -0.00592329  0.        ]
 [-0.00592329  0.05317288  0.        ]
 [ 0.          0.          0.02      ]]
--------------------------------------
Kalman Filter Err:  18.349820543394383
Measured Err:  16.900663359808963

#Basic Imports
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

#Measurement
Hz = 100.0 # Frequency of Vision System
dt = 1.0/Hz
T = 1.0 # s measuremnt time
m = int(T/dt) # number of measurements

px= 0.0 # x Position Start
py= 0.0 # y Position Start
pz= 1.0 # z Position Start

vx = 10.0 # m/s Velocity at the beginning
vy = 0.0 # m/s Velocity
vz = 0.0 # m/s Velocity

c = 0.1 # Drag Resistance Coefficient
d = 0.9 # Damping

Xr=[]
Yr=[]
Zr=[]
for i in range(int(m)):
    accx = -c*vx**2  # Drag Resistance
    
    vx += accx*dt
    px += vx*dt

    accz = -9.806 + c*vz**2 # Gravitation + Drag
    vz += accz*dt
    pz += vz*dt
    
    if pz<0.01:
        vz=-vz*d
        pz+=0.02
    if vx<0.1:
        accx=0.0
        accz=0.0
        
    Xr.append(px)
    Yr.append(py)
    Zr.append(pz)

#Add noise
sp= 0.1 # Sigma for position noise

Xm = Xr + sp * (np.random.randn(m))

Ym = Yr + sp * (np.random.randn(m))
Zm = Zr + sp * (np.random.randn(m))

fig = plt.figure(figsize=(16,9))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(Xm, Ym, Zm, c='gray')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.title('Ball Trajectory observed from Computer Vision System (with Noise)')
# Axis equal
max_range = np.array([Xm.max()-Xm.min(), Ym.max()-Ym.min(), Zm.max()-Zm.min()]).max() / 3.0
mean_x = Xm.mean()
mean_y = Ym.mean()
mean_z = Zm.mean()
ax.set_xlim(mean_x - max_range, mean_x + max_range)
ax.set_ylim(mean_y - max_range, mean_y + max_range)
ax.set_zlim(mean_z - max_range, mean_z + max_range)

#cv2 kalman
import cv2
v = dt
a = 0.5 * (dt**2)
kalman = cv2.KalmanFilter(9, 3, 0)

kalman.measurementMatrix = np.array([
        [1, 0, 0, v, 0, 0, a, 0, 0],
        [0, 1, 0, 0, v, 0, 0, a, 0],
        [0, 0, 1, 0, 0, v, 0, 0, a]
    ],np.float32)

kalman.transitionMatrix = np.array([
        [1, 0, 0, v, 0, 0, a, 0, 0],
        [0, 1, 0, 0, v, 0, 0, a, 0],
        [0, 0, 1, 0, 0, v, 0, 0, a],
        [0, 0, 0, 1, 0, 0, v, 0, 0],
        [0, 0, 0, 0, 1, 0, 0, v, 0],
        [0, 0, 0, 0, 0, 1, 0, 0, v],
        [0, 0, 0, 0, 0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 1, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 1]
    ],np.float32)

kalman.processNoiseCov = np.array([
        [1, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 1, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 1, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 1, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 1]
    ],np.float32) * 0.007

kalman.measurementNoiseCov = np.array([
        [1, 0, 0],
        [0, 1, 0],
        [0, 0 ,1]
    ],np.float32) * sp

kalman.statePre = np.array([
                                [np.float32(Xm[0])], [np.float32(Ym[0])], [np.float32(Zm[0])]
                               , [np.float32(0.)], [np.float32(0.)], [np.float32(0.)]
                               , [np.float32(0.)], [np.float32(0.)], [np.float32(0.)]
                           ])

mp = np.array((3, 1), np.float32) # measurement
tp = np.zeros((3, 1), np.float32)
xt = []
yt = [] 
zt = []
for i in range(m):
    mp = np.array([
        [np.float32(Xm[i])],
        [np.float32(Ym[i])],
        [np.float32(Zm[i])]
    ])
    kalman.correct(mp)
    tp = kalman.predict()
    xt.append(float(tp[0]))
    yt.append(float(tp[1]))
    zt.append(float(tp[2]))

fig = plt.figure(figsize=(16,9))
ax = fig.add_subplot(111, projection='3d')
ax.plot(xt,yt,zt, label='Kalman Filter Estimate', c='green')
ax.plot(Xr, Yr, Zr, c='red', label='Real')
ax.scatter(Xm, Ym, Zm, c='blue', label='Noise')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.legend()
plt.title('Ball Trajectory estimated with Kalman Filter')

# Axis equal
max_range = np.array([Xm.max()-Xm.min(), Ym.max()-Ym.min(), Zm.max()-Zm.min()]).max() / 3.0
mean_x = Xm.mean()
mean_y = Ym.mean()
mean_z = Zm.mean()
ax.set_xlim(mean_x - max_range, mean_x + max_range)
ax.set_ylim(mean_y - max_range, mean_y + max_range)
ax.set_zlim(mean_z - max_range, mean_z + max_range)